El Blog de Mate: 2011

martes, 7 de junio de 2011

EVENTOS DEPENDIENTES

Si se extraen aleatoriamente 2 cartas de diamantes de una baraja: primero una y luego la otra, SIN reposición.

Pd: 13
      52
                               P=PAxPB     P= 13 x 12 = 156          P= 0.5
                                                     52    51    2652
Pd2: 12
        51

EVENTOS INDEPENDIENTES

2 eventos son independientes si la ocurrencia de uno no afecta la probabilidad de que ocurra el otro.

Calcula la probabilidad de que al tirar un dado obtenga un número impar y que al tirar una moneda salga águila.

P= PAxPB

PA=1,3,5,     S=1,2,3,4,5,6
PA=3
      6

PB= moneda S= águila, sol
P=1
    2

     P= 3 x 1 = 3 = .25
          6    2   12

PROBABILIDAD DE EVENTOS COMPUESTOS

Si se lanza un dado, cuál es la probabilidad de obtener un número par o un número mayor que 4.
S=1,2,3,4,5,6
PA= 2,4,6       PA=3
                         6                 P= 3+2-1
                                                6 6 6

PB=5,6          PB=2                 P=4            P=0.66
                         6                    6

FORMULA --->   P= PA+PB-(PAyPB)

BLOQUE X PROBABILIDAD

VARIABLE: es una magnitud que puede tomar cualquier valor según las circunstancias.
ALEATORIO: es un suceso o un evento que está regidopor el azar.

Las variables se dividen en 2: variables aleatorias discretas y continuas.
Las variables discretas son las que toman un número limitado de valores.
Las variables aleatorias continuas,son las que toman cualquier valor dentro de un intervalo.
Ejemplo:
espacio muestral 2 dados: 1,2,3,4,5,6
                                      1,2,3,4,5,6

P=n <-- número de casos favorables
   m <-- número de casos posibles

S <-- espacio muestral

Ej: calcula la probabilidad de que al tirar un dado, el número que caiga sea par.

S:1,2,3,4,5,6
Casos favorables: 2,4,6

P=3   P= 0.5
   6

MEDIDAS DE DISPERSION

Los datos de medidas de dispersion o de variabilidad nos inidican cuánto se desvían los datos de la media.
Algunas de las medidas de dispersión más usuales son:
-rango, amplitud o recorrido (R)
-Desviación estándar (S)
-Varianza (S2)
-Desviación media (DM)

RANGO: el rango es la diferencia entre el dato mayor y el dato menor. Ej: calcula el rango del siguiente conjunto de datos.

8,6,2,4,5,6,7,8,9
R= 9-2
R=7

DESVIACION ESTANDAR: o desciación tipo se define como la raíz cuadrada de los cuadrados de las desviaciones(diferencia) de los valores de la variable respecto a su media.

no agrupados

agrupados

VARIANZA: se calcula casi automaticamente al calcular la desviación estándar y se define con el cuadrado de la desviación estándar.

MEDIDAS DE TENDENCIA CENTRAL

Las medidas de tendencia central son las siguientes:
-media aritmetica x (valor medio)
-mediana (el valor central)
-moda (valor más frecuente)

MEDIA: es también conocida como el promedio aritmético, se obtiene el promedio sumando todos los valores y dividiendolos entre el # total de datos.
Ej: Juan tiene las siguientes calificaciones 9,8,7,6,7,9,8,7 ¿cuál es su promedio?

Datos: 8
x=9+8+7+6+7+9+8+7              x=61
             8                               8

x= 7.6

MEDIANA: la mediana de un conjunto finito de valores, ordenados jerarjicamente,es aquel valor que divide al conjunto en 2 partes iguales. Para calcular la mediana de un conjunto de datos no agrupados se deben seguir los siguientes pasos:
1.Ordenar los datos de manera ascendente a descendente
2.Si el # de datos es impar, la mediana es el dato que está en medio
3.Si el # de datos es par se tienen 2 daos centrales y la mediana es la media de esos 2 valores.

Si los datos son agrupados, la mediana se determina del siguiente modo:
1. Se localiza la posición de la mediana, para eso es necesario construir una distribución de frecuencias acumuladas.
2.Se aplica la siguiente fórmula
        Me= LMe(N/2-fa) cMe
                           fMe

Me: mediana          LMe:Limite inferior del intervalo de clase donde se encuentra la
                                     mediana.

N:numero de datos
fa:suma de las frecuecias anteriores a la clase donde se encuentra la mediana.
fMe:la frecuencia de clase donde está la mediana.
CMe:es la amplitud(tamaño) de clase donde está la mediana.

martes, 3 de mayo de 2011

ESTADISTICA

La estadística es la rama de las matemáticas que se ocupa de reunir, organizar y analizar uno o más conjuntos de datos numéricos en forma ordenada.
La estadística se divide en dos, la descriptiva y la inferencial.
La estadística descripitiva tiene por objeto recolectar, presentar y describir datos numéricos.
La estadística inferencial se ocupa de los métodos para la toma de decisiones.

En la estadística se utilizan 2 métodos para recopilar información, uno es la aplicación de encuestas y otra la observación directa.
La información o datos obtenido puede ser de dos tipos: cualitativos y cuantitativos.
La información que se obtiene debe presentarse ordenada y organizada, para est se utiliza una tabla conocida como tabla de frecuencias.

Población: conjunto de todos los elementos de un grupo que se estudia.
Muestra: es un subconjunto de la población.
Variable: características de interés que presentan los elementos de una población o una muestra.
Dato: valor de la variable asociado a un elemento de una población o muestra.

-Los límites extremos de cada clase se les llama límite inferior y superior.
-Existen también límite real inferior y superior, los cuales se obtienen sumando el límite superior de un intervalo de clase con el límite inferior de la clase siguiente y dividiendolos entre 2.
-La marca de clase es el punto medio de cada clase y se obtiene sumando los límites de clase y dividiendo entre 2.
-El tamaño o amplitud de clase es la diferencia entre los límites reales de clase o la diferencia entre las marcas de clase.
-Frecuencia acumulada, son las que resultam de sumar cada frecuencia con la frecuencia de la clase contigua superior.
-La frecuencia relativa son las que resultan de dividir cada frecuencia entre el número total de observaciones y multiplicar el resultado por 100.

BLOQUE IX "Estadística"

TASAS E ÍNDICES

Tasa:es una razón entre 2 magnitudes con distintas unidades
Razón: forma de comparar 2 cantidades y se expresa com una fracción reducida.

A una tasa cuyo denominador es 1 se le llama tasa unitaria. Por lo tanto podemos definir una tasa como la razón entre 2 magnitudes que tienen diferentes unidades.

Ej. Escribe la razón 10kg de sal por $5 como tasa unitaria, ¿cuántoskg de sal puedes comprar por $1?

Razón ---->   10kg         2kg            Compro 2kg de sal por $1
                         $5            $1

INDICE
Un índice es una medida que informa acerca de los cambios de valor que experimenta una variable o magnitud en 2 situaciones, una de cuales se toma como referencia. La comparación generalmentes e hace por medio de una división.
A la situación inicial se le llama periodo base, y a la situación que queremos comparar se le llama periodo actual o corriente.
El indice se calcula    i= xt
                                  x0

Donde x0 ---> magnitud en el periodo base y xt el valor de la magnitud que queremos estudiar.
El índice es un número con el cual representamos convencionalmente una determinada cualidad o fenómeno

sábado, 30 de abril de 2011

PERÍMETROS Y ÁREAS.

Propiedades de los ángulos

1. En toda circunferencia la medida del angulo central es igual a la medida del arco comprendida entre sus lados.

M<AOB=AB

2. La medida del ángulo interior en una circunferencia es la semisuma de los arcos comprendidos entre sus lados y sus prolongaciones

M<ABC=1/2(arco AC+ arco DE)

3. En toda circunferencia la medida del ángulo inscrito es igual a la mitad del arco comprendido entre sus lados

M<ABC=1/2arco AB

4. En toda circunferencia la m< seminscrito es igual a la mitad del arco comprendido entre sus lados

M<ABC=1/2arcoADB

5. La medida del ángulo exterior a una circunferencia es igual a la semidiferencia de los arcos comprendidos entre sus lados.

M<ABC=1/2(arcoAC-arcoDE)

TEOREMA DE LA RECTA TANGENTE.

si una recta es tangente a una circunferencia, entonces esta es perpendicular al radio trazado al punto de tangencia.

Angulo central. Es el que tiene su vértice en el centro de la circunferencia y sus lados son radios
Angulo interior: es el que tiene su vértice dentro de la circunferencia.

Angulo inscrito. Es el que tiene el vértice en la circunferencia y está formado por 2 cuerdas.

Angulo seminscrito: es el que tiene el vértice en la circunferencia y está formado por una cuerda y una tangente

Angulo exterior. Es el que tiene su vértice fuera de la circunferencia y está formado por dos secantes o dos tangentes o una secante y una tangente.

circunferencia

Circunferencia: es una figura plana y cerrada formada de puntos equistantes de un punto fijo llamado centro
Circulo: es la superficie plana limitada por la circunferencia
Radio. Segmento que une al centro con cualquier punto de la circunferencia
Cuerda: todo segmento rectilíneo que une 2 puntos de la circunferencia
Diámetro: es la cuerda que pasa por el centro
Secante: es la recta que corta a la circunferencia en dos puntos cuales quiera.
Tangente: toda recta en el mismo plano, que toca a la circunferencia en un solo punto llamado punto de tangencia.
Arco: parte continúa de la circunferencia
Flecha: segmento perpendicular a la cuerda que une al punto medio con el arco subtendido por ella.

Leyes de los senos y cosenos

*Leyes de los senos y cosenos*

o Ley de senos

La ley de los senos nos dice que la razón entre la longitud de cada lado y el seno del ángulo opuesto a él en todo triangulo es constante.

Es decir, en todos los triángulos los lados son proporcionales a los senos de sus ángulos opuestos.

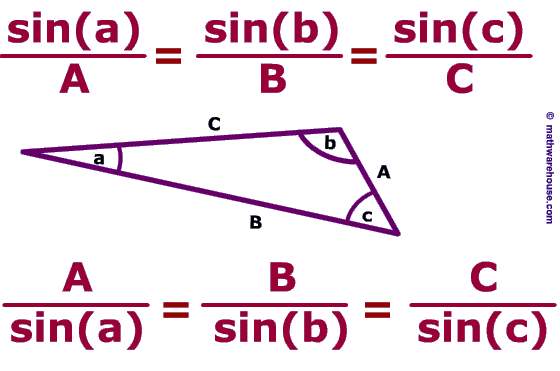formula .

o ley de los cosenos

La ley de los cosenos es una generalización del teorema de Pitágoras en los triángulos no rectángulos.

En general, cuando nos proporcionan 2 lados y el ángulo que forman dichos lados o 3 lados utilizamos la ley de los cosenos.

En toda triangulo, el cuadrado de un lado cualquiera es igual a la suma de los cuadrados de los otros 2 lados, menos el doble producto de estos lados por el coseno del angulo comprendido entre ellos.

IDENTIDADES TRIGONOMETRICAS

Las identidades son igualdades que expresan las propiedades de las operaciones o de los simbolos operativos.
Para las funciones trionometricas exiaten 8 identidades fundamentales,que se dividen en 3 grupos: identidades recíprocas, identidades pitagóricas e identidades de división.