Una igualdad entre2 expresiones algebraicas separadas por el signo(=)
7x+6=x+3
Incógnitas
Son las literales (x,y,q) que intervienen en las expresiones algebraicas, que forman la ecuación y cuyos valores numéricos se desea encontrar
Dominio de definición de una ecuación
Es el conjunto de los números reales que pueden formar las incógnitas de una ecuación
Identidad
Es todo igualdad que se verifica para todos los valores del dominio de las incógnitas
Ecuación condicional
Es toda ecuación que es valida solo para ciertos valores de las incógnitas
Ecuaciones equivalentes
2 o mas ecuaciones son equivalentes cuando tienen el mismo conjunto solución
En este blog te ayudaremos con todas tus dudas sobre matematicas...
domingo, 24 de octubre de 2010
Factorizacion
Es escribir una expresión como producto. la técnica mas simple es encontrar un factor común en todos los términos.
PROCEDIMIENTO GENERAL
1.- Buscar el factor común
2.-Examinar el número de términos
a)2 términos:observar si es diferencia de cuadrados
b)3 términos: ver si es trinomio cuadrad
3.- Factorizar las veces que sea necesario
eJEMPLO: a2-b2=(a-b)(a+b)...diferencia de cuadrados
a2+-2ab+b2=(a+-b)2...termino cuadrado perfecto
FACTORIZACION DE TRINOMIOS
AL MNULTIPLICAR BINOMIO DE UNA VARIABLE SE OBTIENE UN TRINOMIO
PRODUCTO.
(X+2)(X+3)=X2+5X+6
PROCEDIMIENTO GENERAL
1.- Buscar el factor común
2.-Examinar el número de términos
a)2 términos:observar si es diferencia de cuadrados
b)3 términos: ver si es trinomio cuadrad
3.- Factorizar las veces que sea necesario
eJEMPLO: a2-b2=(a-b)(a+b)...diferencia de cuadrados
a2+-2ab+b2=(a+-b)2...termino cuadrado perfecto
FACTORIZACION DE TRINOMIOS
AL MNULTIPLICAR BINOMIO DE UNA VARIABLE SE OBTIENE UN TRINOMIO
PRODUCTO.
(X+2)(X+3)=X2+5X+6
Binomios con termino común
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
Formula
(X+Y)N=XN+NXN-1Y+N(N-1)/2XN-2Y+N(N-1)/2 (N-2)XN-3+......
+N(N-1)/2(N-2)/3...N-(N-2)/N-1XN-(N-1)YN-1+YN
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
Formula
(X+Y)N=XN+NXN-1Y+N(N-1)/2XN-2Y+N(N-1)/2 (N-2)XN-3+......
+N(N-1)/2(N-2)/3...N-(N-2)/N-1XN-(N-1)YN-1+YN
Exponente o potencia
Toda número elevado a una potencia implica la multiplicación del mismo tantas veces como lo diga el exponente
Ejemplo(3)=3x3=9
(3)=3x3x3=27
(3)=3x3x3x3=81
Reglas de los exponentes
1.- La multiplicacion de 2 cantidades de la misma base es igual a tomar la misma base y sumar
Ejemplo: am . an=am+n
2.- La division de 2 cantidades de la misma base. es igual a tomar la misma base y restar los exponentes
Ejemplo: am/an=am-n
3.- La multiplicacion de 2 o mas cantidades cuales quiera esta elevada a una potencia, todos los factores toman el mismo exponente
Ejemplo: (a por b)m es igual ambm
4.- Si la division de 2 cantidades cuales quiera esta elevada a una potencia tanto el numerador como el denominador toman el mismo exponente
Ejemplo: (a/b)m= am/bm
5.- Si una expresión exponencial se eleva a ua potencia, se toma la misma base y se multiplican os exponentes
Ejemplo: (am)n=am.n
6.- Toda la expresión con exponentes negativo se anula y es igual a su reciproco
Ejemplo: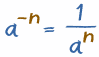
7.- Toda cantidad a la potencia cero es = a 1
Ejemplo: ao=1
8.- Una numero elevado a la una potencia fraccionaria es igual a la raiz d e se número
Ejemplo: am/n= es igual a la raix cuadrada de an m
Ejemplo(3)=3x3=9
(3)=3x3x3=27
(3)=3x3x3x3=81
Reglas de los exponentes
1.- La multiplicacion de 2 cantidades de la misma base es igual a tomar la misma base y sumar
Ejemplo: am . an=am+n
2.- La division de 2 cantidades de la misma base. es igual a tomar la misma base y restar los exponentes
Ejemplo: am/an=am-n
3.- La multiplicacion de 2 o mas cantidades cuales quiera esta elevada a una potencia, todos los factores toman el mismo exponente
Ejemplo: (a por b)m es igual ambm
4.- Si la division de 2 cantidades cuales quiera esta elevada a una potencia tanto el numerador como el denominador toman el mismo exponente
Ejemplo: (a/b)m= am/bm
5.- Si una expresión exponencial se eleva a ua potencia, se toma la misma base y se multiplican os exponentes
Ejemplo: (am)n=am.n
6.- Toda la expresión con exponentes negativo se anula y es igual a su reciproco
Ejemplo:
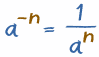
7.- Toda cantidad a la potencia cero es = a 1
Ejemplo: ao=1
8.- Una numero elevado a la una potencia fraccionaria es igual a la raiz d e se número
Ejemplo: am/n= es igual a la raix cuadrada de an m
Reducción de Términos Semejantes
Consiste en sustituir 2 o mas términos semejantes por uno solo, que resulta de la suma o resta algebraica de sus coeficientes numéricos multiplicados npor su parte literal.
1) tienen el mismo signo
5a+3a= 8a -7a-7a=-14a -3a-7a=-10a
2) reducción de términos semejantes que tienen diferente signo
-10m+7m=-3m 5x-7x= -2x -7w+7w= 0
3) reducción de 3 términos o mas semejantes
a) Reducir a un solo término todos los que tienen signo +
b) reducir a un solo termino todos los que tienen signo -
c) aplica paso 2
a)3a+a=4a b) -8a-6a= -14a C) 4a-14a=-10a
1) tienen el mismo signo
5a+3a= 8a -7a-7a=-14a -3a-7a=-10a
2) reducción de términos semejantes que tienen diferente signo
-10m+7m=-3m 5x-7x= -2x -7w+7w= 0
3) reducción de 3 términos o mas semejantes
a) Reducir a un solo término todos los que tienen signo +
b) reducir a un solo termino todos los que tienen signo -
c) aplica paso 2
a)3a+a=4a b) -8a-6a= -14a C) 4a-14a=-10a
Transformaciones algebraicas
Expresión algebraica:
Cualquier expresión que indica una o varias operaciones algebraicas
Ejemplo: 7x-6
3a+y
Cualquier expresión que indica una o varias operaciones algebraicas
Ejemplo: 7x-6
3a+y
Termino algebraico
Un término algebraico es una expresión compuestas por números y letras; relacionadas entres si, mediante las operaciones de suma
Ejemplo: 5x
3ab
Elementos de un termino:
EL SIGNO (+,-)
LA PARTE LITERAL (M,N,O,U)
EL COEFICIENTE NUMÉRICO (5,6,3,1)
Grado:
El grado de un termino es la suma de los exponentes de sus factores literales.
Ejemplo. 9n1
Termino semejante:
Dos o mas términos elevados en los mismos exponentes:
Ejemplo: 3b,b
5xy,98xy
viernes, 22 de octubre de 2010
Multiplicación de polinomios
Polinomio por polinomio
(a+b)(x+y+z)
(a+b)(x)=ax+bx
(a+b)(y)=ay+ax
(a+b)(z)=az+bz ax+bx+ay+by+az+bz
Monomio por polinomio
Para efectuar esta operación se utiliza la propiedad distributiva de la multiplicación
Ejemplo: a(b+c+d+e)= ab+ac+ad+ae
3x2(2x3-7x2-x+6)
3x2(2x3)=6x5
3x2(-7x3)=-21x4
3x2(-x)=-3x3
3x2(6)=18x2
Monomio por monomio
En la multiplicacion de 2 o mas monomios se aplican las reglas de los signos y leyes de los exponentes y seguimos los siguientes pasos
1.- Se determina el signo del producto
2.- Se multiplican por los coeficientes numéricos
3.- Se multiplican las partes literales
Ejemplo:(3x2y)x(4xy4)=+12x2+1 y1+4
= +12x3y5
(-6m2 n4y)(-2mn2y4)=12m3n6y5
Suscribirse a:
Comentarios (Atom)