*Leyes de los senos y cosenos*
La ley de los senos nos dice que la razón entre la longitud de cada lado y el seno del ángulo opuesto a él en todo triangulo es constante.
Es decir, en todos los triángulos los lados son proporcionales a los senos de sus ángulos opuestos.
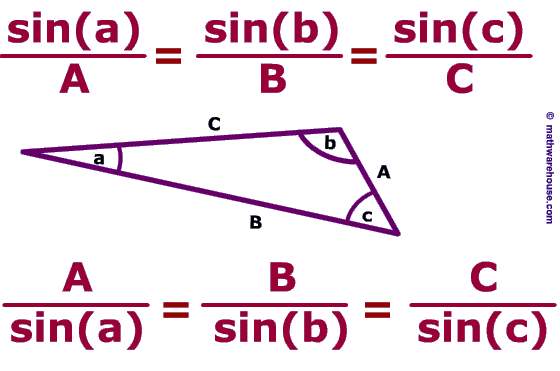 formula .
formula .La ley de los cosenos es una generalización del teorema de Pitágoras en los triángulos no rectángulos.
En general, cuando nos proporcionan 2 lados y el ángulo que forman dichos lados o 3 lados utilizamos la ley de los cosenos.
En toda triangulo, el cuadrado de un lado cualquiera es igual a la suma de los cuadrados de los otros 2 lados, menos el doble producto de estos lados por el coseno del angulo comprendido entre ellos.


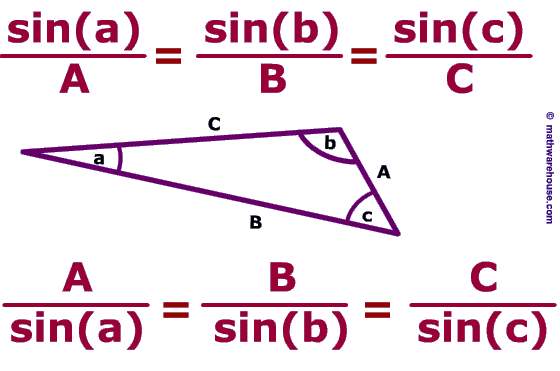 formula .
formula .